• • •
"Mike and Jon, Jon and Mike—I've known them both for years, and, clearly, one of them is very funny. As for the other: truly one of the great hangers-on of our time."—Steve Bodow, head writer, The Daily Show
•
"Who can really judge what's funny? If humor is a subjective medium, then can there be something that is really and truly hilarious? Me. This book."—Daniel Handler, author, Adverbs, and personal representative of Lemony Snicket
•
"The good news: I thought Our Kampf was consistently hilarious. The bad news: I’m the guy who wrote Monkeybone."—Sam Hamm, screenwriter, Batman, Batman Returns, and Homecoming
April 25, 2011
Seriously, Don't Stop Eating Those Bananas.....
By: Aaron Datesman
I have many problems with the Linear Dose Model, some of which I have discussed before. For the last several posts, I have been teasing apart one of the less-obvious problems: the model ignores statistical effects which absolutely must come into play at low dose rates.
Interestingly, the assumption of linearity is at the root of this problem. The model assumes that 50 individual interactions separated in time by minutes, hours, or even years have the same effect on the cell and on the organism as would 50 interactions occurring all at once. Although this is absurd, I suspect that the authors of the BEIR VII report find it "computationally convenient".
Because I think this is a hard topic to understand, I'm going to explain it using an accurate but ridiculous comparison. You are driving a rocket-powered automobile on the Pennsylvania Turnpike. It's a fantastic vehicle, of course - very fast! - but since it's rocket-powered, it's licensed by the state, and monitored rather closely. If you are caught exceeding the speed limit, the cops will take away your rocket.
This is a dangerous situation for you because your entry time is stamped on your turnpike ticket. If you arrive at a turnpike exit 130 miles from where you entered in less than two hours, you obviously exceeded the speed limit at some point. Therefore, you make the sensible choice to make the whole trip at 500mph, but spend two hours reading apocalyptic Christian literature sold to you by Methodists at the Somerset rest stop.
Of course, you blew past the speed limit by nearly a factor of ten; but your average speed was less than 65 mph. So, you get to keep the rocket ship. The situation with average dose and local dose is pretty much the same.
To be specific, apparently the human body typically enjoys 40,000 decays of radioactive Potassium-40 per second. This is naturally occurring, just part of living, and won't even go away if you build yourself a lead-lined bunker with filtered water and industrial air scrubbers. So, in evaluating whether statistical effects are important and should be considered, let's ask whether than level of activity is ever exceeded by 5%. Will we commonly see 42,000 decays per second?
You can apply Gaussian statistics (Poisson statistics generalize to the easier-to-use Gaussian for large numbers of decays) to calculate, quite straightforwardly, that the probability of this 5% excursion from the average is around 2 x 10^-9. That's a pretty small number. In a year, among a population of 300 million human beings, it will almost certainly occur; but not very often.
And it's a small excursion. Compare 5% to the thought experiment with 4 atoms of deadly Schwarzium, where there was a 1/16th chance that we would obtain double the number of expected decays. In radioactive decay, as in wealth, there is a degree of certainty in large numbers.
So, why am I prattling on about statistics? A factor of 5% is scarcely anything to worry over. The answer, in short, is that we just assumed that the decay of an unstable potassium atom in your big toe can give you brain cancer.
Alpha, beta, and gamma particles are fundamentally different things; they interact with matter in different ways, and have distinct biological effects. For the purposes of this post, however, it's sufficient to note that they possess different ranges in tissue. For instance, beta particles emitted by the decay of Potassium-40 dissipate all of their energy over a distance of around 1mm from the point of emission. The possible biological effects of the decay are limited approximately to that region, and should not be averaged over the entire body.
To put this concisely, the "interaction volume" for beta emission is around 1 cubic millimeter. We should be benchmarking the decay rate against this volume, and not at all against the volume of the entire body. Since the human body has a volume of around 70 million mm^3, it is appropriate to discuss the decay rate as 40,000/70,000,000 = 6x10^-4 decays/sec over 70 million interaction volumes. It is not appropriate to discuss it as 40,000 decays over 1 human body.
6x10^-4/sec is a low rate of average decay per interaction volume, for which statistical effects absolutely must be considered. So, I went ahead and, using Poisson statistics, did some considering. The graph below shows the probability of seeing multiple decays in an interaction volume for a range of low values of the average rate of decay. (Note that the vertical axis is logarithmic.) These probabilities are small numbers; they become even smaller for larger numbers of decays; and they increase as the average decay level increases. All of this is perfectly sensible.
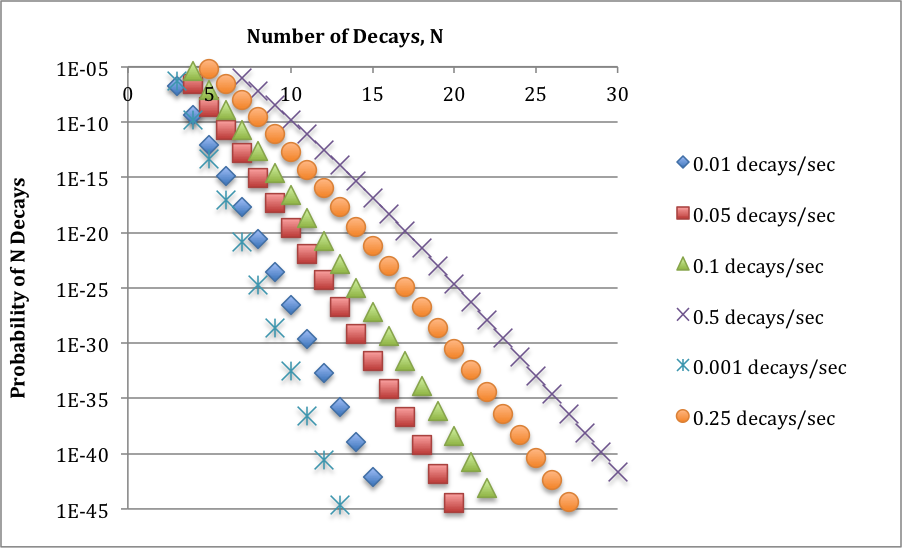
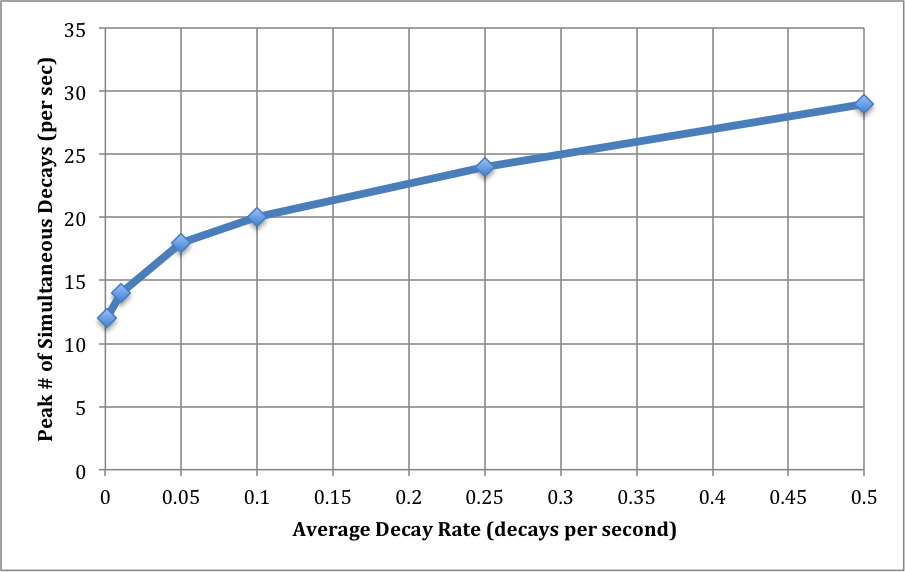
There is next a small piece of magic, which I will explore further in a subsequent post. The interesting probability level is around 10^-40. (It might be different by several orders of magnitude. This is envelope-back stuff.) Basically, this reflects the fact that we run the decay experiment over many, many interaction volumes: the 70 million cubic millimeters in a human body, the number of seconds in a year, and the number of bodies in a population. For each value of the average decay level, then, I read off the number of decays N at a probability of around 10^-40.
This is the largest number of decays we are likely to see in a one-second interval as the result of the low average decay rates we've examined. I've graphed this out below. I think it's remarkable that, at a decay rate of 0.001/sec (that's 1 decay in 16 minutes), we will almost certainly find an interaction volume with 10 decays in a one second interval. That's a difference of 10,000x.
Examining just the whole-body dose overlooks this effect altogether. Does that seem appropriate, or wise? I should reiterate again that this is very basic, undergraduate-level physics. I should be able to say to any physicist, "I'm examining the biological effects of shot noise in very dilute systems of radioactive particles," and he or she should understand much of what I've discussed here very quickly. Asking a physicist this is an experiment you should feel free to do yourself, by the way.
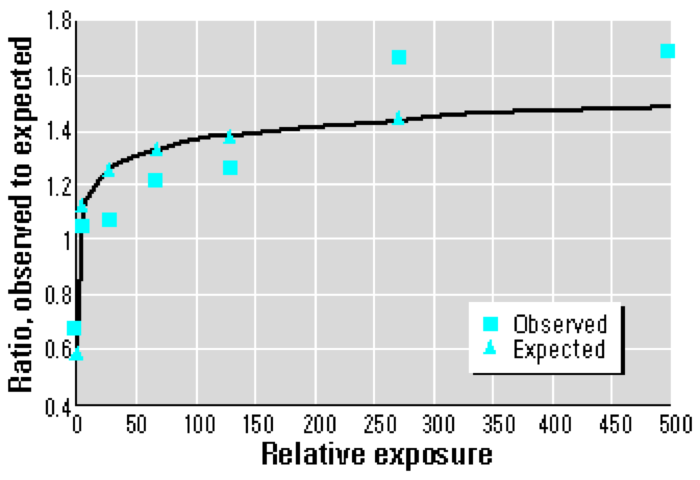
You should compare the graph above to the squares on the graph of excess lung cancer deaths from TMI, which I reproduce below. It is worthwhile to give some thought to the similarity, remembering that the measurements on the graph below no doubt deserve significant error bars.
— Aaron Datesman
Posted at April 25, 2011 12:52 AM
I usually cannot come close to understanding your posts about physics.
Nevertheless I enjoy reading them.
Posted by: jharp at April 25, 2011 02:07 AMI think you need a new hobby.
Susan - tell me about it!
Posted by: Aaron Datesman at April 25, 2011 07:55 AMLooking at your first graph, pick number of decays equals to 10.
The 0.5 decays per second gives a probability of 1 E -10.
As best I can read it, the .05 decays per second gives a probability of around 1 E-21 or so.
So a factor of ten decrease in the average decay rate gives, for those particular values, a decrease of about 100 billion in the rate of that particular rare event.
It seems to me that you're talking about some sort of threshold model where N decays in a given volume in a short amount of time will trigger cancer. If that's the case, I think your first graph argues in the opposite direction from what you want to show. You get your final graph looking along a given horizontal line (1 E-40) and I think the more interesting way to look at it is how many events of a given magnitude you are likely to get for a given average decay rate (which means looking at a given vertical line).
Posted by: Donald Johnson at April 25, 2011 08:52 AMI wish I had taken a bit of physics every time I read one of these posts. But I'll pass on the "ask a physicist experiment" because I just don't think it's humane to experiment on physicists.
Thanks for all that math and science, Aaron.
I actually already did try the ask a physicist experiment; well, I passed the blog on to one, but I'll wait a bit longer before asking what he thinks. I'm curious though.
Posted by: godoggo at April 25, 2011 11:30 AM@Donald Johnson - Thanks for reading carefully. I'm glad that you seem to get it.
This is a case where the math would be clearer than words are. The vertical axis on the second graph (Peak # of Simultaneous Decays) does not represent rare events - they're common. The message is this: at an average decay rate of 0.05/s, most people will experience at least one event of around 20/s in at least one "interaction volume" in their bodies.
(There's a bit of a number error in the post, I now realize. I used the interaction volume for alpha particles rather than beta. The shape of the curve is not affected, but the numbers on the axis should be different. Since it doesn't change the conclusion substantively, I think I'll leave it as it is.)
I don't actually yet know exactly what to think about this....I only began to think about this issue very hard after reading the BEIR VII report. It's shocking that our low-dose risk assessments are simply linear extrapolations from high doses. And it's TERRIFYING that some pretty simple undergraduate physics suggests rather strongly that the safety assessment approved by the National Academy of Sciences simply cannot be correct.
That said, this is what I am beginning to suspect: the mortality rate from cancer is proportional to the dose delivered in high-dose events (not to the average dose, and not to the whole-body dose). Since cells can repair low levels of damage (and do all the time), this hypothesis seems highly plausible to me.
I probably wouldn't think to question it if it were stated by an expert. Which I am not. But I am trained in physics, and very basic physics definitely shows that high doses to individual cells can result from low average decay rates.
Posted by: Aaron Datesman at April 25, 2011 11:49 AMAaron, I'm disagreeing with you.
If I understand you correctly, you are hypothesizing that cancer might be triggered when a cell is hit multiple times in a small period of time. But that sort of thing is much more likely to occur at high dose rates than low ones as shown by your first graph. There's a nonlinearity here, but it's one that makes small dose rates much less dangerous than a linear model would. Poisson statistics are also simple enough you can do estimates if you choose small numbers. For instance, suppose cancer is induced if there are two or more decays in a small volume in a given time when the average number of decays in that volume in that time period is lambda, where lambda is much less than one. Then you can show that the approximate chance of getting those two decays in that time is (lambda squared divided by two). (That's also the rough estimate for two decays or more). That means if you cut the dose rate by a factor of ten the probability of cancer-inducing events is cut by one hundred. In your top graph I picked N = 10--then if you cut the average dose rate by a factor of ten the number of N=10 events is cut by a factor of many billions (as best I can tell from your graph).
This seems like a model for arguing that when you cut the average dose rate you decrease the chance of cancer-inducing events by more than the linear model would suggest.
You get the linear model if you just assume that cancer is induced in most cases by one hit by one photon (or beta particle or whatever). Assuming it has to be multiple hits in a short time span gives a nonlinear model, but I think it makes low dose rates much safer than the linear model suggests.
Posted by: Donald Johnson at April 25, 2011 12:54 PM@DJ - Yes, I thought about it that way for quite a while, too. But: there's another piece of math you're missing. There are 70 million interaction volumes in the human body, and 30 million seconds in a year. If your binary cancer model is correct (get two disintegrations, get cancer), then the probability of getting cancer is
1-(1-lambda^2/2)^(2x10^15).
I think, if you play with this expression, you will discover interesting things. I do not think you'll discover that the cancer probability goes down by 100x if the average decay rate lambda goes down by 10x.
This has been rather confusing for me, too. That's why I decided to string it along slowly over several posts. The strategy may not be working, however.....
Posted by: Aaron Datesman at April 25, 2011 01:50 PMAaron, you can lead a horse to water, but you can't make it think. (badumCHI)
Posted by: N E at April 25, 2011 03:33 PMThat's funny! But the lesson seems to be that, in at least I few cases, I can!
Posted by: Aaron Datesman at April 25, 2011 03:57 PMOkay, adding in your corrections and generalizing.
Let Pc be the probability of inducing cancer in one interaction volume in one time unit.
Let N be the number of interaction volumes times the number of time units (your 2 x 10^15)
The probability of not getting cancer = (1-Pc)^N
The probability of cancer = 1 - (1-Pc)^N
There are two ranges to look at. If NPc is greater than or equal to 1, the probability of cancer is close to 1.
If NPc
Anyway, this stuff is cool to think about, but I can't believe the people in field haven't done all sorts of theoretical models. I don't think everyone would be a prisoner of The Man and refuse to think outside the approved box.
Part of my post got dropped. I think it was when I typed much much less than (and the computer thought it was html language maybe).
Here's the missing part--
If NPc is much less than 1, then the probability of getting cancer is about NPc and if we go back to my two hit model that would be
N lambda squared over 2. So I'm back where I started (though multiplying by N). Possibly I goofed in the math.
@DJ - Responding just to the last comment about THE MAN, yeah, I can't believe it either. In fact, in the small amount of reading I've done in the biological literature, when scientists do experiments with alpha emitters and small numbers of cells, they use Poisson statistics and seem aware of these sorts of issues.
Nobody generalizes that to human health effects, however....what we get instead is the linear model and extrapolations from high doses. FROM THE NATIONAL ACADEMY OF FRIGGIN' SCIENCES. It's groupthink, in my opinion. Also: disgraceful.
Posted by: Aaron Datesman at April 25, 2011 05:43 PMMr. Johnson:
Continuing on Mr. Aaron's remarks, Mr. Aaron is someone who is in the field who is doing this work. I doubt he is the only one. The primary motive in our society is profit and if a scientist does something that would be unprofitable, there are a lot structures to marginalize that scientist's work. Until there if a profit motive in figuring out an accurate model for health risks from radiation, it won't be developed. The structures in place are so subtle that those effected are likely not to be noticed by scientists. I know this not because I'm too smart to know exactly what these structures are but because classical economics tells me so. Incidentally, there was very little hard science on climate change until there was a market for it.
Posted by: Benjamin Arthur Schwab at April 25, 2011 07:03 PMSomeone complained about this before, I'm confused by the labeling of the last graph is confusing. y is "ratio. observed to expected," and x is "relative exposure?" Can someone make this clear?
Posted by: godoggo at April 25, 2011 10:02 PMEh, you know what I meant.
Posted by: godoggo at April 25, 2011 10:03 PM"Anyway, this stuff is cool to think about, but I can't believe the people in field haven't done all sorts of theoretical models. I don't think everyone would be a prisoner of The Man and refuse to think outside the approved box."
I kind of agree with Benjamin Arthur Schwab's response above, to a point, but I think Donald Johnson's quote above is more fascinating. Or more accurately, I think what it touches upon is fascinating. Whole dissertations could be written on the orthodoxy of thought in different fields and how it works, both to cause creativity and to reduce it, because I think it works both ways. That certainly has to do with material forces--Marx was right about that--but not in such a crude way as BAS posits. I've gone about as far with it as I have time for in understanding it all, and already I'm swimming in strong currents again that don't allow me to look back for the source of the river. In any field, those who swim against such currents generally drown. I have no doubt it's the same in physics as it is in economics and law and politics and engineering and everythign else I've ever heard of. So I believe what Donald Johnson can't believe, and more to the point, my experience has led me to disagree with him. In fact, though something as silly as "The Man" has nothing to do with it, I think his reference to "The Man" reveals that the currents that shape the course of our thought are real.
Posted by: N E at April 25, 2011 10:03 PMNot everything in life is about power politics and quite a few people (maybe most) who go into science do it because they're interested in it. One thing I don't like about politics--anyone's politics--is the totalitarian way it has of presuming to explain the entire world, science or anything else be damned. If you have a political ideology you don't need science or any sort of data--you just need to know how it fits into your political scheme and the truth is made manifest. Free market economists are the world champions in this. They take their fracking ideology and shove it into every situation and generally try to force the world to fit. It's dehumanizing and also stupid. But they aren't the only ones. In fact, maybe lefties and righties have more in common here than either acknowledges.
I suspect a lot of people who go into the field of radiobiology are probably interested in the subject. I know, it's weird, but I bet a lot of people in the field really want to know how radiation induces cancer and they probably sit around from time to time and try to think about how it might work.
Posted by: Donald Johnson at April 25, 2011 11:17 PMLooking at BEIR VII, there are quite a few pages on various mathematical models for the effects of radiation. In fact, there's way more technical detail than I would even want to try to wade through. It might all be wrong, of course.
Posted by: Donald Johnson at April 26, 2011 12:05 AMDonald Johnson
True enough, but sitting around from time to time and trying to think about how things might work isn't enough of a commitment, or looked at differently, enough of an opportunity. I agree that many people are interested in thinking, and they are interested in the truth, and they aren't typically corrupt, and I think that may even be especially true of many scientists. I just don't think that ONLY power politics or highly political ideology can have a controlling influence on thought. The basics of social control of most people are simple and obvious enough, but I don't think the whole story is simple at all. There are a lot of tributaries to this river, and a lot of eddies in it.
Plus, there actually are people who do what you call thinking outside the box, even very qualified and brilliant people. Aaron isn't the only person in the world who thinks deeply about neglected issues. Idiots with orthodox ideas get lots of public attention, as do people with views that are useful for other purposes, but people who raise serious questions of the wrong sort usually get marginalized. I get the feeling you have read very widely, as widely or more widely than I have, but there is just too much to know now for anyone, even the Davincis of this age (whoever they are). It's easy to keep information from people just because there is so much information. We are all too specialized--look how few people can follow what Aaron is writing. You and perhaps a handful of others seem to be coming close--I certainly am not. There is not even a real need to suppress ideas.
Anyway, peace be with you and your cats. I have mostly abandoned thinking about these issues for more ordinary battles more in keeping with the part of me that is, in general, not to be fucked with. "I'd rather be pissed than depressed" is my motto. Juvenile, I know.
Posted by: N E at April 26, 2011 12:49 AM@godoggo - Yeah, sorry. I haven't been tracking comments closely and I'm surprised that somebody with epidemiology knowledge hasn't answered this.
The answer, I think, is that Mangano plotted excess over expected. I would write this as O-E/E, myself. This means that 0.4 = 40% above the expected rate, 1 = twice the rate, and 2 would = three times the expected rate.
Which is a pretty small effect, unless the population is large. Which is the critique the authors of the article offered about Mangano's response.
Maybe this gets lost in the ten or so posts I've written about this, but what gets me so riled is that our safety assessments about radiation are based on an ASSUMPTION. It's worse that, in this case I can show that the assumption must be wrong - but why are we making safety judgments based on ASSUMPTIONS at all?
Posted by: Aaron Datesman at April 26, 2011 11:08 AMHola,
erais visitados por el pensamiento excelente
Miato
Okay, NE, peace. And you remembered I have cats--that goes a long way towards smoothing things over. Actually just one cat now and he's on the downward path, being 20 years old.
Posted by: Donald Johnson at April 26, 2011 04:52 PMDonald Johnson
20--that's impressive, almost the oldest I've heard of. I myself find it easy to get attached to the little mousers. We actually have three cats ourselves, down from our high of four, and they've all been around about 8 years now, so I'm hoping they all make it to 20. I was a dog person at first, but cats have won me over. They are much more polite than my kids, and smarter than most dogs. The Egyptians were on to something there.
Posted by: N E at April 28, 2011 11:09 AM


