• • •
"Mike and Jon, Jon and Mike—I've known them both for years, and, clearly, one of them is very funny. As for the other: truly one of the great hangers-on of our time."—Steve Bodow, head writer, The Daily Show
•
"Who can really judge what's funny? If humor is a subjective medium, then can there be something that is really and truly hilarious? Me. This book."—Daniel Handler, author, Adverbs, and personal representative of Lemony Snicket
•
"The good news: I thought Our Kampf was consistently hilarious. The bad news: I’m the guy who wrote Monkeybone."—Sam Hamm, screenwriter, Batman, Batman Returns, and Homecoming
April 22, 2011
Schwarzium Pennies
By: Aaron Datesman
The field of radiation physics is a mess, unit-wise. We have rems and rads, Sieverts, Grays, Curies, and Becquerels, just off the top of my head, with micro-this equal to 10 milli-that – or maybe the other way around. The fundamental quantities, though, are energy (in Joules) and rate (in inverse time). The latter is the basic meaning of the Curie – 1 Ci is equal to 37 billion decays occurring in one second.
It’s a weird unit, though, because as it’s applied it often seems to measure concentration. In the conventional sense of number of molecules per volume, however, the Curie does not measure concentration directly. For instance, a measurement of 0.01pCi/m^3 of Cs-137 certainly sounds small – it represents one decay in a cube one meter on a side in 45 minutes – but that isn’t really the whole story. There are 1.17 million atoms of cesium in that cube.
And, while it is extraordinarily unlikely, all of those million-odd unstable cesium nuclei could spontaneously decay all at once. (This is why I would prefer to refer to concentration rather than dose.)
Now, in the real world, one million simultaneous decays against an expected level of one decay will never occur. However, there are absolutely statistical effects at play in low-dose health effects which seem to have been ignored in the field. Wednesday’s Gedankenexperiment is a first step in the direction of examining this oversight and trying to understand what it might mean.
The solution to the puzzle relies on the statistical (one could also say random, or stochastic) nature of radioactive decay. In a time span equal to one half-life, each individual atom does indeed have a 50% chance of undergoing decay. However, this does not at all mean that exactly and only two of the four atoms of Schwarzium have decayed after five minutes. It’s necessary to employ some simple statistics to analyze the situation correctly. We’ll use pennies to represent atoms of Sw – heads for no decay, tails for decay.

Since each atom has two possible states, there are 2^4=16 possible combinations. To figure out the decay probabilities, we simply have to count how many of those 16 possible combinations correspond to 0,1,2,3, and 4 decays.
0 decays – zero Tails: only 1 combination1 decay – one Tail: 4 combinations (Tail in positions 1,2,3, or 4)
2 decays – two Tails: 6 combinations, (remainder from 16 total)
3 decays – three Tails: 4 combinations
4 decays – all Tails: only 1 combination
Therefore, the probability of 3 or 4 decays occurring in one half-life is (4+1)/16 = 31.25%. You probably survived……but it was closer than you might have thought. This is (yet another) example of how statistics can kill you, I guess. The real takeaway, though, is this: the decay process is random, not deterministic. Sometimes, in a given interval of time, many more decays will occur than are strictly expected based on the average value of the decay background. Benchmarking against the average value of the disintegration rate (0.01 pCi/m^3) obscures this reality.
When a large number of nuclei simultaneously disintegrate inside the body, the surrounding tissues receive a tremendous dose of energy - even though the concentration, and the average decay level - are low. As far as I can tell, the linear dose no-threshold model does not account for this reality whatsoever.
Over the next several posts, I will argue that stochastic effects make low concentrations of radioactive materials much more dangerous than is commonly assumed. The fundamental insight supporting this assertion is this: as the average number of decays in a given volume increases (because the concentration of radioactive materials increases), the probability of a large number of excess decays (above the average rate determined by the half life) occurring decreases. This is basic statistical mechanics - not controversial in the least.
The dose increases, of course, because the average number of disintegrations has gone up – but the likelihood of extreme events goes down. The net effect of these two conflicting trends is a slow increase in the frequency of dangerous, large-dose events with increasing (but small) levels of radioactive contamination in the environment. In fact, I’m reasonably sure the relationship is logarithmic. If I were better at math, I would have that fully worked out by now.
The first step will be to examine what choice of “interaction volume” is biologically appropriate. It doesn’t make any sense at all to consider the so-called “whole-body” dose when the range of an alpha particle in tissue is only 50 microns.
(By the way, the relationship between the number of cesium atoms in the cube and the half-life of cesium is
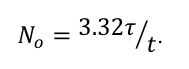
The relationship holds for any radioactive substance which undergoes one disintegration in the time interval t. Interestingly, for a given measurement of activity, the longer the half-life, the more material there must be.
Looking back at this graph, then, one reaches the non-obvious conclusion that there was more Cesium than Iodine in the fallout from Fukushima recorded in Illinois on 3/22/11. The half-life of Cs-137 is 30 years, while the half-life of I-131 is only 8 days. The ratio of the measured activity levels was about 6 in favor of Iodine, but the half-life of Cesium is more than 1000 times longer.)
— Aaron Datesman
"And, while it is extraordinarily unlikely, all of those million-odd unstable cesium nuclei could spontaneously decay all at once."
Just to note--this is a physicist's "unlikely", which is subtly different from the layman's "unlikely". It's entirely possible that a glass of lukewarm water would spontaneously transform into a set of ice cubes floating in hot water, but it's profoundly unlikely in the same sense.
Posted by: grendelkhan at April 22, 2011 07:45 PMI wish to describe the situation I as understand it and this point in the series. I am a laymen: I am not a scientist nor am I a doctor but I do have some science training and some medical training. The the extent to which I am wise I am a better person for my disparate training but to the extend to which I am arrogant, my little training in these fields makes me dangerous. I will admit to being quite arrogant.
I've been fallowing this discussion, Mr. Aaron and also the comments. It is something which interests me in an academic sense but I am still more scared of all of the chemical poisons around me then the radioactive poisons. I suspect that more cancers are caused by chemical byproducts of industrialization then by radioactive ones but I have been reminded of my ignorance on the issue of radioactivity and approach the problems of it differently because of your efforts. I thank you for them.
I don't think that this particular post questions the linear low dose model but questions the amount of dose one receives. This is dependent on the definition of dose, of course. What you describe here, I believe is a link between exposure and dose. For my own discussion I will take exposure to be in the vicinity of radioactive products or the internalization of radioactive products and a dose to be the absorption of a radioactive decay product by the body.
Given the discussion of yourself and others, I suspect that dose fallows a logistical harm profile: given that the body has absorbed a certain amount of decay products, initially the body can cope with it, then the coping mechanisms break down and the higher the dose the more it negatively effects things, then when there starts to be a risk of death, the risk approaches a flat-line of guaranteed death. At any point the model could be locally approximated by a straight line but in a logistical model and where the high dose is measured, the high dose linear approximation extrapolated downwards to low doses will undoubtedly underestimate harm at a given dose and overestimate a safe threshold. For low doses, however, the model appears to increase exponentially.
From this post, it seams to me that the expected dose received is linear to the amount of exposure but the maximum reasonably expected dose, for small doses, is logarithmic to the amount of exposure (I would think, it should be x+I*sqrt(x) where x is the amount of exposure (in curries) and I is the measure of what is reasonable and has units of root curie and this would hold for the entire range). In either model the expected dose monotonically increases with exposure and the chance of getting N doses also monotonically increases with exposure.
In either case, if both models hold, then the exponential behavior of low dose harm would dominate in determining risk of harm from exposure. It should also be noted that the way exposure happens is important. The route (in the same vicinity of a cloud of gas vs. digestion of an amount of the substance, for example), the chemical properties of the substance, and the byproducts of the substance all matter. It seams that a danger calculation needs to be made for each different isotope and route to have an accurate model but overall a combination should be used to get from exposure to harm which would look mostly logistic for all cases.
One other this to point out, for everyone dosed more then expected for a given exposure there is also likely someone dosed less then expected for a given exposure. For safety purposes, one should use a reasonably high (or reasonable safe) exposure to dose model, but use a linear exposure to dose model for calculating damage expectations once damage has occurred.
Posted by: Benjamin Arthur Schwab at April 22, 2011 08:46 PM"The dose increases, of course, because the average number of disintegrations has gone up – but the likelihood of extreme events goes down. The net effect of these two conflicting trends is a slow increase in the frequency of dangerous, large-dose events with increasing (but small) levels of radioactive contamination in the environment."
Intuitively, I see how the increase in magnitude of large-dose events increases slowly with an increase in concentration at low levels, but it's less obvious how you reach the conclusion that the frequency of large-dose events increases slowly as well.
Posted by: Vinnie at April 22, 2011 09:17 PMActually, the one interpretation I've seen that begins to make sense of the evidence says the underlying reality does not involve chance. Which means the answer to your previous question is, "You killed my brother. Prepare to die."
But the math still has a hole if we assume that all 'worlds' contain conscious observers. So the world where all the cesium decays at once might act like a brief reflection that never comes alive. Ask me again when we figure out what "observer" means.
Posted by: hf at April 22, 2011 10:46 PMhf
My wife just spent half an hour last weekend talking to Inego Montoya's wife by happenstance when in NY, and she told Mrs. Inego that we often use his famous words in our family, which as a bunch of goofballs we do, and she told my wife that they do in their family too. Just thought you might like to know that bit of trivia even though it doesn't involve a cab driver.
As for the science, I've read it several times and am not close to following it all, but I get some of it. All I know for sure is that I could find an expert with good credentials to agree or disagree very impressively with aaron either way if the money was right. I don't think this is so different from how real science works, but I'm not thomas kuhn.
All the different units drive me crazy. Centimeters to inches is too much for me. Aaron is really good at making this stuff comprehensible given that I can get roughly close to almost being able to following along without devoting days and days and days to it. Good job Aaron! The physics for dummies crowd applauds you.
Posted by: N E at April 22, 2011 11:31 PMI
Posted by: Amandasaurus at April 22, 2011 11:56 PMMany professional disciplines use a strange lingo then wonder why the layman in the public does not read it.
Posted by: Dredd at April 23, 2011 10:18 AMI read all of that, and God bless you Mister Datesman, for learning and knowing all that stuff. But now my brain hurts.
Posted by: awesome guy at April 23, 2011 03:31 PMDredd, comments like those are why we can't have nice things.
Posted by: Amandasaurus at April 24, 2011 11:01 AMnice blog, will come back later :-)
Posted by: Anneliese Kleinknecht at April 26, 2011 05:26 AM


