• • •
"Mike and Jon, Jon and Mike—I've known them both for years, and, clearly, one of them is very funny. As for the other: truly one of the great hangers-on of our time."—Steve Bodow, head writer, The Daily Show
•
"Who can really judge what's funny? If humor is a subjective medium, then can there be something that is really and truly hilarious? Me. This book."—Daniel Handler, author, Adverbs, and personal representative of Lemony Snicket
•
"The good news: I thought Our Kampf was consistently hilarious. The bad news: I’m the guy who wrote Monkeybone."—Sam Hamm, screenwriter, Batman, Batman Returns, and Homecoming
April 14, 2011
We All Should Have Paid More Attention to Logarithms
By: Aaron Datesman
I had a little fun with graphs earlier this week. Perhaps you would like to have a little fun, too? If your idea of fun involves inputting tables of mortality statistics into an Excel spreadsheet, then it would be rude of me to keep all the fun to myself! So, why wait for me? Here are the mortality tables (use the code “140-205 Malignant Neoplasms”); and here is the US EIA data on the energy produced by nuclear power plants in the U.S. It will probably be a little while before I finish the analysis myself….
The idea I took away from that thought experiment about cancer rates and fallout (aka “emissions”) from commercial nuclear reactors is this: perhaps the dose relationship (for low doses) is logarithmic rather than linear. Mathematically, this is expressed for the excess death rate and total energy produced simply as
![]()
Since the energy produced is exactly proportional to the number of radioactive fission products created by the process, this is about equivalent to a relationship between dose and harm.
Having trained in physics, I like this – it reminds me of statistical thermodynamics. Although I had mono that semester, it’s rather natural to see a logarithm here – therefore it “feels” right. At a basic level, this is true because of a result known as the Central Limit Theorem. Physics undergraduates ordinarily encounter this in the context of the “random walk” problem, but it’s a universal statement about the distribution of results subject to a large number of statistically independent random events.
Perhaps it was clearer when I said that it “feels” right.
So, the interesting thought is this: perhaps the linear model for low doses should be replaced by a logarithmic dose (or exposure) relationship. Is this crazy? Well, actually I’m not the first person to think of it. The Radiation and Public Health Project made this observation about an evaluation of the health effects of the Three Mile Island accident which was published in 1997:
Plotting the O/E (Observed/Expected) ratios by level of exposure shows that the dose response does not conform to a linear model. Rather, a logarithmic or supralinear curve describes the relationship more accurately, as the greatest per-dose effects occur at the very lowest levels of exposure.
If I understand the graph below correctly, the author (Joe Mangano, whose analysis of thyroid cancer incidence I critiqued here) has fit a logarithmic relationship to the “Observed” data; the quality of the fit is determined by the vertical distance between the squares and triangles.
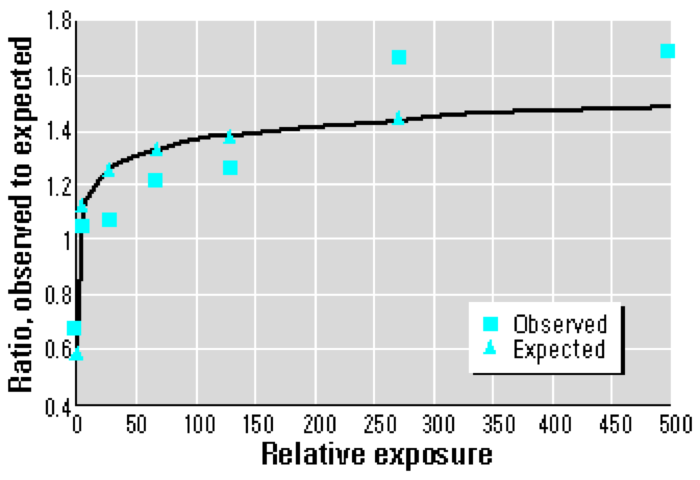
It may not be immediately clear, but a logarithmic model would be a very significant departure from the linear dose assumption upon which our judgments of safety are based. Using a linear model, for instance, reducing the dose by a factor of two reduces the health effects (typically, death) by the same factor. A logarithmic model, however, responds to a factor of two reduction in dose with a reduction in mortality by only an additive factor.
That is: if a logarithmic dose model applies, low doses of radiation are much more harmful than we currently believe.
So, how likely is it that our current operative understanding could be wrong? Well, the notoriously anti-nuclear organization known as the Federal Government of the United States of America has this to say about the health effects of low doses of ionizing radiation:
Since we cannot measure the stochastic [this means random, or non-deterministic, in the sense of the Central Limit Theorem - AD] effects of very low levels of exposure, health physicists must extrapolate the risks from what they know about high levels of exposure. Most radiation protection organizations estimate the risk of health effects from low levels of exposure, all the way to zero exposure, as proportional to those of high levels of exposure.
According to the Environmental Protection Agency, our beliefs about the safety of low levels of radiation are guesses based upon knowledge of the effects of high doses and the assumption of a linear dose model. Fortunately, I guess, we have the opportunity to assess whether that assumption of a linear dose model is correct – by graphing out the mortality statistics from a dangerous experiment we are performing on ourselves.
I actually don’t find that to be very much fun at all.
- Aaron Datesman
I did notice in the last plot of your last post that in adding the mortality, you used a linear mortality scale, while the electricity plot was presumably on a logarithmic scale. The good fit here suggests a logarithmic relationship. However, the range of mortality rates was not large, so a power law relationship might work as well. A power law relationship (y = a x^b) has the advantage that y is 0 when x is 0, which isn't true for a logarithmic relationship (for which y goes negative for x less than 1).
I might mention also that linear is used in two ways. One is that the relationship between two variables can be described by a straight line (y = a x + b). The other (which is the sense that you are using it) is that it can be described by a straight line through the origin (y = a x). Except for the lowest point, the data you plot could be described by the former, but not the latter.
Posted by: Mike B. at April 15, 2011 08:36 AMYou refer to the problem of finding evidence to support a causality. That seems to be an insurmountable problem when looking at an issue like this one. Low doses of radiation might have out-sized effects on human health, but there's no way to do an experiment. One might look at plants and animals that live in the vicinity of a nuclear facility, but the effect of cellular changes on short-lived species might be impossible to detect. Any effect on long-lived species such as trees must be fairly subtle since there's no obvious ring of mutated trees around nuclear plants.
"Feelings" aren't good enough. The anti-evolution people "feel" evolution is wrong and conclude that, therefore, it must in fact BE wrong. This is a trap good scientists fall into - to some degree - and hopefully briefly - on a regular basis.
Reminds me of taking electromagnetics in college and working with the exposed guts of a microwave. I asked the professor if it wasn't just a bit dangerous, since we had to strip a crap load of shielding to expose everything and he replied, "The effects of microwave radiation are unknown on the human body". There was a silence in the class room, and I said, "So... they might be harmful" and he replied, "The effects of microwave radiation are unknown on the human body" and we went on with the class.
The dangers our science uncovers haven't been around long enough for us to have evolved the proper danger response - like snakes or heights.
Posted by: Phaedrus at April 15, 2011 09:11 AM@ edb -
Your point is well taken, but when I say it "feels" right, what I mean is that the health effects problem is analogous in many ways to the random walk problem. Therefore it would be sensible to observe the same functional relationship in radiation health effects, based on the mathematically provable foundation of the Central Limit Theorem.
I have to work this out a bit; but it's a method of reasoning by analogy which is very common in the physical sciences. Sometimes it's called "physical intuition".
Perhaps this is the same as a person who believes that evolution "feels" wrong because it's different than what the Book of Genesis says. In some respects, I've spent the last month of my life thinking about the Religion of the High and Most Holy Linear Dose Model.
So in fact I might agree with you.....
Posted by: Aaron Datesman at April 15, 2011 10:58 AMMy idea of fun totally includes inputting tables of mortality statistics into an Excel spreadsheet.
Posted by: Amandasaurus at April 15, 2011 12:36 PMDifferent species respond to radiation in different ways, as seen at Chernobyl (Wired's recent article "Is Chernobyl a Wild Kingdom or a Radioactive Den of Decay?"). Extrapolating from a random species to human beings is not meaningful -- we don't know how sensitive we are or what species we should compare ourselves to.
Posted by: reslez at April 15, 2011 06:13 PMI've always considered log v linear as a plotting device. Especially for issues of dosing. Dose data are simply better behaved when transformed and plotted on a log scale. I'm sure radiation, like any well-behaved drug, goes from minimal to maximal effect over a very narrow dose range, ~10-fold, or even less for radiation.
Posted by: me at April 15, 2011 08:21 PMI mean, you can plot (and fit) data to linear or log functions, but data plotted on log scales is usually prettier...over a wider range of doses...and more informative in terms of revealing subtle differences.
Posted by: me at April 15, 2011 08:31 PMThe vertical axis is label "ratio, observed to expected". Shouldn't the expected values always be at 1? Just wondering.
Posted by: Kaleberg at April 15, 2011 08:51 PMI'd intuitively expect a sigmoid, not a logarithm. After all, the body has some resilience in the face of radiation, but this can obviously be saturated. There's also most likely a maximal harm, e.g. destruction of the gut lining and bone marrow resulting in death shortly after exposure. You can't get much worse than dead, though a really large radiation dose might impart enough energy to kill someone nearly instantly by thermal and related effects.
You seem to be starting from the assumption that even a slight exposure to radiation causes extreme damage. Given the low number of deaths at Three Mile Island, I'd feel more comfortable if you did a similar analysis using the Hiroshima or Chernyobl datasets. (In fact, we know that there is some resilience because so many of the Chernyobl deaths could have been prevented with information and iodine.)
Posted by: Kaleberg at April 15, 2011 08:56 PMAdding some biology to the physics suggests that the curve is neither linear nor logarithmic, but rather a chimera of two (or more) curves, with an inflection point (or range).
Life has evolved on earth in the presence of non-negligible levels of background radiation. As a result, organisms have developed mechanisms to repair the cellular damage caused by radiation (as well as other physical insults). At very low doses of radiation, most cells in an organism will be able to deal with whatever damage might result from such exposure. But as radiation levels rise, cells become overwhelmed, and repair mechanisms can't keep up with the rate of damage inflicted. Thus, at very low doses of radiation, death rates (from cancer, the primary cause of low-to-moderate dose radiation death) are indistinguishable from those caused by background radiation.
As doses rise, radiation damage can overwhelm the cellular damage-repair machinery; here, a second biological effect comes into play. The radiation-induced cellular damage of most interest is damage to DNA, which can lead to cancer--but most DNA damage does NOT lead to cancer. There's a big stochastic factor here--not only do you have to damage DNA, but you have to damage it in the right places in order to cause cancer.
Note that "places" is plural, not singular; thanks to redundancy in biological systems, single mutations don't often lead to cancer--it generally takes two or more DNA defects, or mutations, to produce a cancerous cell. However, for the same reason, your body contains lots of "pre-cancerous" cells--cells which have one DNA defect (from causes other than the radiation in question) which could contribute to the development of cancer. In these cells, a single additional mutation--the right (or wrong, I guess) mutation is enough to "transform" the cell to a cancerous state.
Now, I'm not an expert in radiation biology, but I'd guess that the linear portion of the exposure/cancer curve is the range wherein DNA repair mechanisms are overwhelmed, and rare damage to rare "pre-damaged" cells is the driver of cancer incidence.
As radiation levels rise further, the likelihood of multiple radiation-caused events within a single cell rises. In this realm, we have to start considering that multiple DNA mutations are more likely to be lethal than carcinogenic; we also have to consider other mechanisms of radiation toxicity other than cancer. Here we see more in the way of acute radiation poisoning, and increased rates of cancer among those who survive the acute phase.
And and levels rise even further, acute radiation sickness becomes more lethal--not because of cancer, but because of cell damage. We're no longer concerned with carcinogenicity, but immediate cell death in overwhelming numbers.
In summary, if you were to plot out radiation-related deaths vs. radiation exposure, with the latter as a logarithmic X-axis, I think you'd see a (roughly) sigmoid curve. A flat, but non-zero segment at very low doses, attributable to background radiation and other physical/chemical insults; a rising segment at low-to-moderate doses, attributed to radiation-induced cancers (which will likely show an inflection point as the average rate of DNA mutations/cell rises past 1); and a plateau (100% radiation-induced mortality) due primarily to acute radiation poisoning.
Posted by: jimbo at April 15, 2011 09:31 PMI dunno. Maybe taking the time to explain or even label the axes with some specificity might lure a reader's interest, or perhaps you have no interest in the layperson.
Posted by: Compound F at April 16, 2011 07:30 AMWell, here's yer "Rider-On-A-Pale-Horse" 4ya. War-check, Pestilence-check, Disease-check, but what about the last one? My guess is that John( May GOD bless his name),back in the day when he saw his vision, being a fisherman, with no education in nuclear theory, had NO word for "electromagnetic radiation". Colorless, odorless, no way for the 5 senses to detect, thus Death on an almost transparent horse.
Posted by: Mike Meyer at April 16, 2011 07:05 PMAaron: Can you please explain this graph? What it says. It seems to prove the opposite of what you say. At low doses (between 1 and 250), the squares are below the triangles, which seems to indicate that exposure actually reduces cancer rates! Are you suggesting building nuclear plants that leak small doses of radioactive material to help reduce cancer? :-) What am I missing here?
Also, can you answer kaleberg's point? Why would you have points for observed and expected if you only plot ratios? I don't understand this plot? Or is it a mistake and we're plotting pre-TMI vs. post-TMI? But then why the labels?
Not that it matters but why is log(E) suggestive of a central limit law? Maybe square root or square root of log, or log log. But log alone?
Thanks. Great series, though I have this nagging feeling that the scarcity of data means anyone can interpret it any way they want.
Posted by: bobs at April 16, 2011 09:16 PMAaron, bearing in mind that a) this is from way back in March, and b) I know you've addressed some of these points here and there, I'd be interested in a quick response to this post by a physician on Fukushima, which ends, "I draw two conclusions from all of this. First, while the troubles at Fukushima are by no means trivial, and for that matter aren't yet finished, I think it's a bit premature to write the obituary for nuclear power [yadda yadda...]. Second is that we should try to minimize mammograms!"
Posted by: godoggo at April 18, 2011 04:16 PMDude, jimbo above is describing what's called hermosis.
It's been written about recently by both Orac
http://scienceblogs.com/insolence/
and PZ Myers
http://scienceblogs.com/pharyngula/
in recent time (since Fukushima).



