• • •
"Mike and Jon, Jon and Mike—I've known them both for years, and, clearly, one of them is very funny. As for the other: truly one of the great hangers-on of our time."—Steve Bodow, head writer, The Daily Show
•
"Who can really judge what's funny? If humor is a subjective medium, then can there be something that is really and truly hilarious? Me. This book."—Daniel Handler, author, Adverbs, and personal representative of Lemony Snicket
•
"The good news: I thought Our Kampf was consistently hilarious. The bad news: I’m the guy who wrote Monkeybone."—Sam Hamm, screenwriter, Batman, Batman Returns, and Homecoming
April 06, 2013
Saturday Night Graphs
By: Aaron Datesman
An early commenter to this post made the intelligent suggestion that a graph showing the prediction of the linear dose model would have been helpful. I agree! Here's that graph:
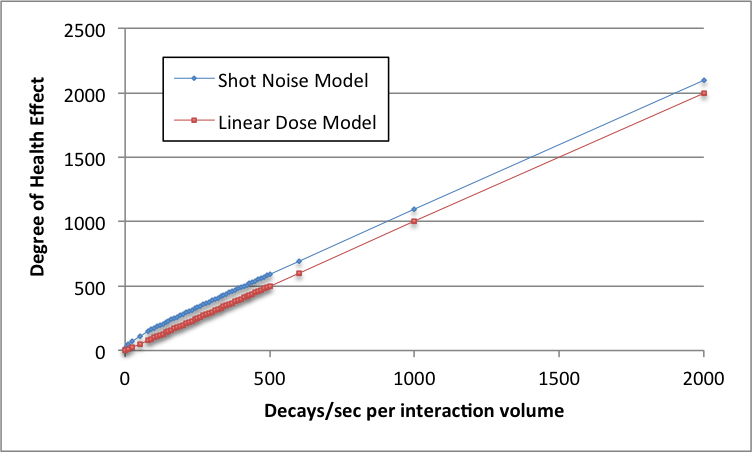
The two curves never truly converge (due to shot noise, there is always an excess equal to half the frequency bandwidth), but they're not significantly different. This indicates that the decay power (determined by the shot noise model) and energy (the fundamental quantity described by dose) are numerically identical. In sum: the linear dose model basically works in this domain.
So, let's extrapolate downward to low doses:
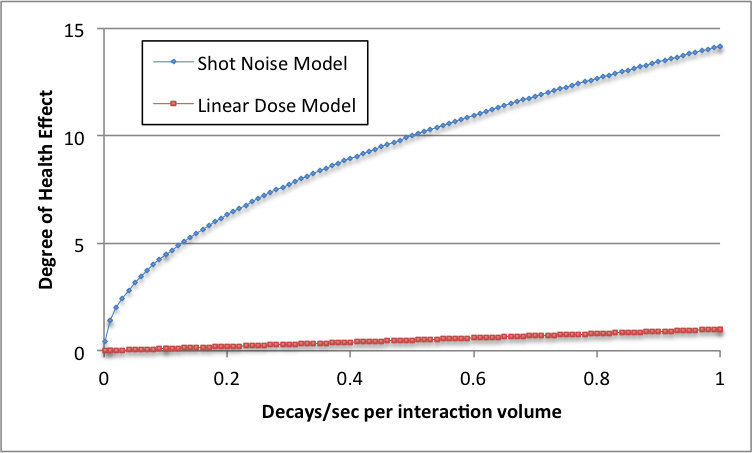
For low decay rates such that the chemical state of the cell is disturbed only about 1% of the time, the linear dose model misses by a factor of around 10. For even lower decay rates (since the square root of N is much bigger than N if N<<1), the relative situation is much worse.
Hm.
— Aaron Datesman
In the context of a meltdown, ionization is going to continue for days, weeks, months or as the facts on the ground show, years, unless OUR cancer victims remove from the area of contamination. The graphs start to match around 1 decay/sec/volume I would guess from figure 2. I'm of the belief that a meltdown would amp up much, much more. I'm also of the belief that, in fact,"normal leakage" far outstrips that 1 decay/sec/volume in the matter of increased cancer casualties&TMI. My contention IS there are no low dose rates around these reactors. Also I contend that to understand a "low dose" at all one must have EXTENSIVE data of background radiation from before July 1945. IMHO, TODAY'S background radiation, world wide, assures there is no such thing as a "low dose" here on planet earth. "Low dosage" is a misnomer except in the context of "Just How Radiation Proof Are YOU?"
Posted by: Mike Meyer at April 7, 2013 02:51 AM@Mike Meyer, it's the shape of the curve more than the numbers. The axis measures decays/sec per "interaction volume", which is a little piece of your body around 1 mm^3 or so in volume.
I don't believe that the doses around TMI were low, but it's possible that the doses which caused these lung cancers were. More on that coming.
Posted by: Aaron Datesman at April 7, 2013 08:39 AMIs the shot noise model simply that only the maximum power matters for the health effect, not the dose? Why would that be the case?
Everyone knows that ionizing radiation occurs in packets--when you have a low dose it means a (relatively) small number of particles shooting through, but the standard assumption is that the chance of inducing cancer would go up linearly with every particle. That makes sense. It may be oversimplified, but it makes sense. One reason it may not be right is that at higher doses there is a disproportionately greater chance of getting two or more particles hitting at the same time. But that's the linear/quadratic model (which ignores the three or more particle cases, but the chances of those go up even higher with dose rate.)
The shot noise model, as best I can tell, seems to be that there is some special significance given to the fact that the average power at low doses is much much smaller than the momentary maximum power, whereas at high dose rates the relative size of the fluctuations drops (meaning maximum power divided by average power drops). But that is just to say that for long stretches of time (long compared to 5 ms) nothing happens, and then a particle shoots through. But everyone knows that. The linear model doesn't claim that at low doses the 1 MeV (for example) of some particle will be delivered a few ev at a time. Once in a very long while two or even more may shoot through, but if those sorts of interactions matter, their number goes up with the square of the dose (or cube, etc...)
It's like saying that if you have two snipers shooting into a crowd (so that every shot hits), one sniper drunk with a muzzle-loading rifle who shoots erratically and the other a WWII Garand who shoots at a relatively steady pace and much faster, the muzzle loader is doing more damage per shot because the fluctuations in the power divided by the average power is greater with the muzzle loading sniper.
Unless I'm misunderstanding the model, of course. Gotta go for now.
Posted by: Donald Johnson at April 7, 2013 09:39 AM@Donald Johnson, sort of. I could graph a curve of the the maximum number of decays Nmax in an interaction volume in a unit of time, and it would look very much like the shot noise model. I posted those curves here in 2011, and I recall you commented on them.
Calculating the power using the shot noise model just accounts for all the Nmax-1, Nmax-2, etc. decays also. This is the accepted method in communications theory, it's absolutely well-known.
And you are correct, all I'm saying is that the number of free radicals tracks the power, not the energy. The only thing that's even interesting here is that I've pointed out that the power of a random signal that is wide-sense stationary must be calculated using the appropriate mathematics - not linearly extrapolated.
I'll post the math soon, and you can review it. This idea is absolutely mainstream.
Posted by: Aaron Datesman at April 7, 2013 10:13 AMAaron, the blue shot-noise curves that you have graphed in this new post contradict your claims about low-dose radiation effects and the Linear Non-Threshold theory.
You are claiming that health effect per amount of radiation exposure follow the blue shot-noise curve, not the purely linear red curve. Fine, let’s go with that.
That means that the current LNT approximations, which are derived from empirical observations of high-dose radiation effects, must also come from the blue curve in its high-dose, approximately linear region. After all, Nature doesn’t follow the blue curve at low doses and then switch to the red curve at high doses; it has to follow the blue curve all the way up.
But according to your own graph, the tangent line to the blue curve’s high-dose region, when extended all the way down to zero, is higher than the nonlinear portion of the blue curve at low doses, because in the low-dose region your blue curve bends sharply downward away from that extrapolated high-dose tangent line. So the low-dose portion of your blue shot-noise curve is “sublinear” compared to the tangent line extrapolation from the high-dose linear portion of the same curve. But that tangent line from the high-dose portion of the curve is exactly what LNT follows in estimating low-dose risks.
Therefore, if you are correct and the blue shot-noise curve is the true curve describing all the radiation risks at every dose range, then the low-dose region must be “sublinear” compared to LNT, and LNT is overestimating radiation effects at low doses. When we use LNT to predict low-dose risks, we would then get an upper bound prediction; the true low-dose risks would be smaller than LNT predicts.
So your larger policy complaint that LNT underestimates low-dose radiation effects does not agree with your own blue shot-noise curves. Your blue curves predict sub-linear radiation risks with respect to LNT, not supra-linear.
Hmm... When unsure of the proper application of Shot Noise, do you listen to a guy who writes commentary for The Baffler and In These Times, or a guy who has a doctorate in EE, was a staff scientist at Argonne National Lab and is now at NASA?
Sorry Will, I'm putting my money on you only having first heard of Shot Noise when Aaron posted about it the other day and immediately raced to Wikipedia to see what it was.
Posted by: Aric at April 7, 2013 01:28 PMAh, but now I see my own error.
If LNT derived from the blue shot-noise curve is calculated by including the origin point, (0,0) on the graph, then its slope would deviate slightly downward from the tangent line at high-doses. If that’s the case then LNT might indeed underpredict shot-noise by some small amount.
It probably makes little difference empirically. LNT equations are dominated by the points at high dosages; shifting the low-dose points has little effect on the curve. At such small dosages, the dose-response is empirically imponderable anyway; the effects are essentially “zero with error bars.”
@ Donald Johnson,
In your sniper analogy, I cannot see why a given shot from a muzzle-loader at a low and erratic rate of fire would do more damage than a shot from a Garrand at a higher and steadier rate of fire.
That does sort of seem like what Aaron's shot-noise theory is saying, which is why I don't understand it.
Posted by: Will Boisvert at April 7, 2013 02:08 PMShould I want to cut a piece of steel with a chisel, I MUST have a chisel that's harder than the surface I desire to cut. I can take my little tap hammer and tap until closing time or break out the ole 9 pounder and in a couple of minutes, WE're done. Either way the chisel MUST be harder than the object to be cut.
So, just exactly, what is it that hits the cellular wall and cuts it, that ionizes those molecules and breaks the chemical bond. What kind of chisel is that, exactly.
Hey Will- Just FYI, Aaron actually replied to your final comment on the last post. Well worth a read, including this part:
"Will Boisvert is wasting the time of everybody who reads these comments, not only me. Everyone who participates should understand this."
@Mike Meyer, is that a Zen question? It kind of has an answer.
The chemical bonds have an energy of ~50eV. (Doesn't matter what an eV actually is, it's just a unit of energy.) An ionization event releases around 500,000eV.
That's the chisel. Were you really asking?
Posted by: Aaron Datesman at April 7, 2013 08:08 PMAaron Datesman; Yes, I was asking. I was thinking more along the lines of an actual collision event between the Radiated particle or energy and the electron of the soon-to-be ionized atom. Is the "bullet" (chisel) an electron, proton, neutron, inducted magnetic field, pure energy, something else that moves that electron from orbit?
Posted by: Mike Meyer at April 7, 2013 08:24 PM@Mike Meyer - yes! Most of those, at different times.
Alpha particles are two protons and two neutrons. Beta particles are electrons. Gamma rays and x-rays are two names for photons (little packets of energy). Neutrons are also very damaging. And there are fission products, too, for instance if there is uranium in your body that interacts with a cosmic ray.
Magnetic fields, well that's a different thing.
The means of interaction with the body are all different, but a root sort of effect is chemical changes in water molecules due to ionization. The theory I'm describing postulates that chemical changes in the body drive the ultimate health effect.
Posted by: Aaron Datesman at April 7, 2013 09:34 PMAaron Datesman: THANK YOU. ALL YOU have said makes sense&I agree with especially the part about disturbed chemical reactions. After all, once one has microwaved all the water out, its no longer a cup of coffee.
Posted by: Mike Meyer at April 8, 2013 01:24 AM


